研究发现统计物理定理在量子世界中也有效

波恩大学的物理学家通过实验证明，统计物理学的一个重要定理适用于所谓的“玻色-爱因斯坦凝聚体”。他们的结果现在可以测量量子“超粒子”的某些特性，并推断出否则难以观察到的系统特征。该研究现已发表在《物理评论快报》上。

假设在你面前有一个装满未知液体的容器。您的目标是找出其中的粒子(原子或分子)由于其热能而随机前后移动的程度。但是，您没有显微镜来观察这些称为“布朗运动”的位置波动。

事实证明你根本不需要它：你也可以简单地将一个物体系在一根绳子上，然后将它拉过液体。您必须施加的力越大，液体就越粘稠。而且它越粘稠，液体中的粒子平均改变它们的位置就越小。因此，给定温度下的粘度可用于预测波动的程度。

描述这种基本关系的物理定律是波动耗散定理。简而言之，它指出：从外部扰乱系统所需施加的力越大，如果您不理会它，它自身随机(即统计)波动的幅度也就越小。

“我们现在首次证实了该定理对一组特殊量子系统的有效性：玻色-爱因斯坦凝聚体，”波恩大学应用物理研究所的JulianSchmitt博士解释道。

由数千个光粒子组成的“超级光子”

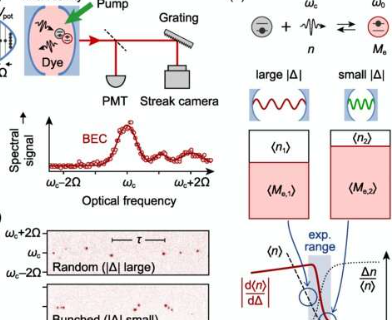
玻色-爱因斯坦凝聚物是由于量子力学效应而产生的奇异物质形式：在某些条件下，粒子，无论是原子、分子，甚至是光子(构成光的粒子)，都变得无法区分。成百上千个它们合并成一个“超级粒子”——玻色-爱因斯坦凝聚(BEC)。

在有限温度的液体中，分子随机来回移动。液体温度越高，这些热波动就越明显。玻色-爱因斯坦凝聚体也会波动：凝聚粒子的数量会发生变化。并且这种波动也随着温度的升高而增加。

“如果波动耗散定理适用于BEC，那么它们的粒子数波动越大，它们对外部扰动的响应就越敏感，”施密特说。“不幸的是，通常研究的超冷原子气体BEC的波动数量太小，无法检验这种关系。”

然而，MartinWeitz教授的研究小组(其中Schmitt是初级研究小组组长)研究由光子制成的玻色-爱因斯坦凝聚体。对于此系统，该限制不适用。“我们让BEC中的光子与染料分子相互作用，”这位物理学家解释道。当光子与染料分子相互作用时，经常会发生分子“吞噬”光子的情况。染料因此变得充满活力。它可以稍后通过“吐出”一个光子来释放这种激发能。

低能光子被吞噬的频率较低

“由于与染料分子的接触，我们的BEC中的光子数量显示出很大的统计波动，”物理学家说。此外，研究人员可以精确控制这种变化的强度：在实验中，光子被困在两个镜子之间，以乒乓球的方式来回反射。

镜子之间的距离可以变化。它变得越大，光子的能量就越低。由于低能光子不太可能激发染料分子(因此它们被吞噬的频率较低)，因此凝聚光粒子的数量现在波动较小。

波恩物理学家现在研究波动的程度如何与BEC的“响应”相关。如果涨落-耗散定理成立，这种灵敏度应该随着涨落的减小而降低。

“事实上，我们能够在我们的实验中证实这种效果，”施密特强调说，他也是波恩大学跨学科研究领域(TRA)“物质”和卓越集群“ML4Q-物质和量子计算之光。”

与液体一样，现在可以从更容易测量的宏观响应参数推断玻色-爱因斯坦凝聚体的微观特性。“这为新应用开辟了一条道路，例如复杂光子系统中的精确温度测定，”施密特说。